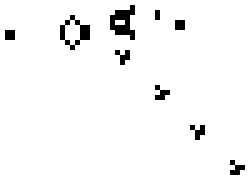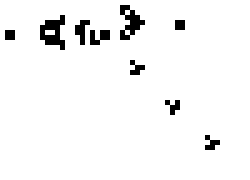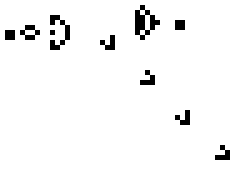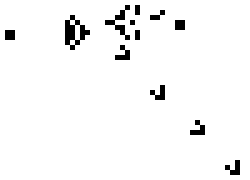Experimenting with Conway's Game of Life
I recently discovered Conway's Game of Life, "a cellular automaton devised by the British mathematician John Horton Conway in 1970." as described by Wikipedia. This is a "game" with a simple set of rules. There is a grid, and each grid can be alive or dead. Living cells with two or three live neighbors remain alive and dead cells with three live neighbors become alive. Those are the only rules, and yet with these rules unexpected emergent complexity can arise as illustrated by the below gif [1].
The simple rules and emergent depth fascinated me, and this has been used as an example of emergent complexity, a metaphor for how complexity can exist in our own universe, and as an educational tool. It is also a chaotic system, in that slight changes to the initial conditions can dramatically affect later states in unpredictable ways. The game has no definite history, as the rules cannot simply be played backwards. Any one state could have many possible previous states. All of these features offer easy ways to understand parallel concepts in the real world.
If you want to experiment with Conway's Game of Life I have created a simple version on canvas.alexlockhart.me that uses the left arrow key to proceed the clock and clicking on cells makes them come alive. The benefit of this version as apposed to the others is that I am providing it as a web component so that it can be easily reused on the web. Simply install the "canvas-play" npm package and use it on your own web project.
There is also playgameoflife.com which provides more features but has a bit of an older look and does not allow close in zooming. For more features and controls along with some large scale randomization you can try out https://copy.sh/life. Google even has an easter egg of Conway's Game of Life when searching for that exact phrase.
Some have have described emergent features of the game such as "energy". Cells can be alive or dead, but a group of cells can have "energy" when they have the ability to move and yet retain their relation to one another. This is also shown in the scene above. The below shape has the ability to move on it's own.
The simple rules and emergent depth fascinated me, and this has been used as an example of emergent complexity, a metaphor for how complexity can exist in our own universe, and as an educational tool. It is also a chaotic system, in that slight changes to the initial conditions can dramatically affect later states in unpredictable ways. The game has no definite history, as the rules cannot simply be played backwards. Any one state could have many possible previous states. All of these features offer easy ways to understand parallel concepts in the real world.
If you want to experiment with Conway's Game of Life I have created a simple version on canvas.alexlockhart.me that uses the left arrow key to proceed the clock and clicking on cells makes them come alive. The benefit of this version as apposed to the others is that I am providing it as a web component so that it can be easily reused on the web. Simply install the "canvas-play" npm package and use it on your own web project.
There is also playgameoflife.com which provides more features but has a bit of an older look and does not allow close in zooming. For more features and controls along with some large scale randomization you can try out https://copy.sh/life. Google even has an easter egg of Conway's Game of Life when searching for that exact phrase.
Some have have described emergent features of the game such as "energy". Cells can be alive or dead, but a group of cells can have "energy" when they have the ability to move and yet retain their relation to one another. This is also shown in the scene above. The below shape has the ability to move on it's own.
This concept of energy yet again is illustrative of both philosophic and scientific concepts in our own world. The concept of "energy" is not fundamental to Conway's Game of Life and yet the concept "emerges" out of the rules. Cells can either be alive or dead, that is the "real" thing at the bottom of this games reality. Energy is a way to describe a patterns of live or dead cells. This is easy to understand in this game, and can aid in understanding how things such as heat is an emergent reality in the real world. Molecules have a velocity but are themselves not hot or cold. "Heat" is a way to describe a pattern of molecules.
The metaphors and illustrations that this game provides is immense, and all derive from such simple rules. What might we add to the discussion? I thought we could do a hexagonal version, since hexagon's also can map out a flat 2d surface, but that also has been done on arunarjunakani.github.io/HexagonalGameOfLife. This is quite fascinated, and to me the hexagonal version feels more stable than the square grid version. The below example [2] demonstrates this hexagonal game of life.
We could also imagine changing the rules or even changing the space in which the game takes place. We could play the game on a curved surface so that the space wraps around to itself. And we don't have to limit ourself to a simple sphere, as illustrated on the below Trefoil Knot example.
The sparks of creativity that this simple concept provides is quite amazing!
Attribution
- By Grontesca at the English language Wikipedia, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=2840938
- By Kieff - Own work, CC BY-SA 3.0, https://commons.wikimedia.org/w/index.php?curid=101736
- By Raphaelaugusto - Own work, CC BY-SA 4.0, https://commons.wikimedia.org/w/index.php?curid=52336285